Question

Please help nobody knows the answer to my question. Round to 2 decimal places.

Answer 1

To answer this question we will use the z-score.

Recall that the z-score is given as follows:

`\begin{gathered} z=(x-\mu)/(\sigma), \\ \text{where x is the observed value, }\mu\text{ is the mean, and }\sigma\text{ is the standard deviation.} \end{gathered}`

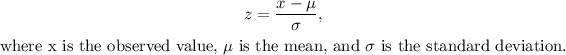
The z-score of 54 is:

`z=(54-50)/(5)=(4)/(5)=0.8.`

The z-score of 56 is:

`z=(56-50)/(4)=(6)/(5)=1.2.`

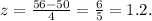
Now, the probability of flipping 54, 55, or 56 heads is the same as the following probability:

`P(0.8Now, recall, that:[tex]P(aNow, from the given table we get that:[tex]\begin{gathered} P(0.8)=0.7881, \\ P(1.2)=0.8849. \end{gathered}`

Therefore:

[tex]\begin{gathered} P(0.8Answer: 0.10.