So we have two planes flying toward each other. Let's use v for the speed of the slower plane. Then the speed of the faster plane is v+40. If we pass to the reference system of the slower plane we have that its speed is 0 and the speed of the other plane is v+v+40=2v+40. So basically we have a problem where one of the planes is stationary whereas the other approaches at 2v+40mph and it takes it 2 hours to travel 1180 miles. Remember that the speed is equal to the distance traveled divided by the time it took the plane to travel that distance. Then we get:

Then we get:
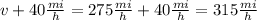
Then the speeds of the planes are 275mph and 315mph.