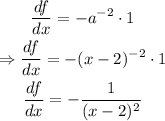Question

Find the derivativef(x) = 1 / (x - 2)

Answer 1

`(df)/(dx)=-(1)/((x-2)^2)`

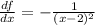
Step-by-step explanation

We want to find the derivative of the given function:

`f(x)=(1)/(x-2)`

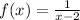
First, we have to rewrite the function as follows:

`f(x)=(x-2)^(-1)`

Next, make the following substitution:

`a=x-2`

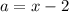
The function now becomes:

`f(x)=a^(-1)`

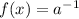
Apply the chain rule of differentiation:

`(df)/(dx)=(df)/(da)\cdot(da)/(dx)`

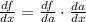
Therefore, we have that:

`(df)/(da)=-1\cdot a^(-1-1)=-a^(-2)`

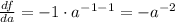
and:

`(da)/(dx)=1`

Therefore, the differentiation of the function is:

`\begin{gathered} (df)/(dx)=-a^(-2)\cdot1 \\ \Rightarrow(df)/(dx)=-(x-2)^(-2)\cdot1 \\ (df)/(dx)=-(1)/((x-2)^2) \end{gathered}`