Question

The distance from the ground of a person riding on a Ferris wheel can be modeled by the equation d equals 20 times the sine of the quantity pi over 30 times t end quantity plus 10 comma where d represents the distance, in feet, of the person above the ground after t seconds. How long will it take for the Ferris wheel to make one revolution?

Answer 1

We have the function d, representing the distance from the ground of a person riding on a Ferris wheel:

`d(t)=20\sin ((\pi)/(30)t)+10`

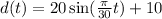
If we consider the position of the person at t = 0, which is:

`d(0)=20\sin ((\pi)/(30)\cdot0)+10=20\cdot0+10=10`

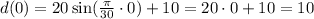
This position, for t = 0, will be the same position as when the argument of the sine function is equal to 2π, which is equivalent to one cycle of the wheel. Then, we can find the value of t:

`\begin{gathered} \sin ((\pi)/(30)t)=\sin (2\pi) \\ (\pi)/(30)\cdot t=2\pi \\ t=2\pi\cdot(30)/(\pi) \\ t=60 \end{gathered}`

Then, the wheel will repeat its position after t = 60 seconds.

Answer: 60 seconds.