Question

Function g is defined as g(x)=f (1/2x) what is the graph of g?

Answer 1

D.

Step-by-step explanation

We know that g(x) = f(1/2x)

Additionally, the graph of f(x) passes through the point (-2, 0) and (2, 0).

It means that f(-2) = 0 and f(2) = 0

Then, g(-4) = 0 and g(4) = 0 because

`\begin{gathered} g(x)=f((1)/(2)x_{}) \\ g(-4)=f((1)/(2)\cdot-4)=f(-2)=0 \\ g(4)=g((1)/(2)\cdot4)=f(2)=0 \end{gathered}`

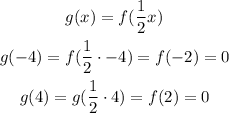
Therefore, the graph of g(x) will pass through the points (-4, 0) and (4, 0). Since option D. satisfies this condition, the answer is graph D.