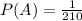Question

Could you help me with this problem?There are 7 acts in a talent show.A comedian, a guitarist, a magician, a pianist, a singer, a violinist, and a whistler.A talent show host randomly schedules the 7 acts.Compute the probability of each of the following events.Event A: The magician is first, the comedian is second, and the whistler is third.Event B: The first three acts are the guitarist, the pianist, and the singer, in any order.Write your answers as fractions in simplest form.

Answer 1

EXPLANATION

For the event B, the order of the first 3 acts doesn't matter.

So, the number of acts taken from the seven acts when the order doesn't matter is calculated using combinations.

`C(m,n)=(m!)/(n!(m-n)!)`
`C(7,3)=(7!)/(3!(7-3)!)=(7!)/(3!4!)`

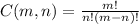
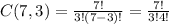
Computing the factorials:

`C(7,3)=(5040)/(6\cdot24)=(5040)/(144)=35`

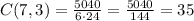
Hence, the number of ways the three acts could be given are 1:C(7,3)

Therefore, the probability of the event B is:

`P(B)=(1)/(35)`

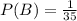
For the event A, the order matters, so the difference between combinations and permutations is ordering. When the order matters we need to use permutations.

The number of ways in which four acts can be scheculed when the order matters is:

`P(m,n)=(m!)/((m-n)!)`
`P(m,n)=(7!)/((7-3)!)=(5040)/(24)=210`

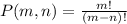
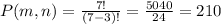
The number of ways the magician is first, the comedian is second and the whistler is third are 1:P(7,4)

Therefore, the probability of the event A is.

`P(A)=(1)/(210)`