Question

I got 4089 for the answer but it was incorrect

Answer 1

Let A be the event "person under 18" and B be the event "employed part-time". So, we need to find the following probability

`P(A\text{ or B) =P(A}\cup B)`

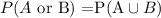
which is given by

`P(A\text{ or B) =P(A}\cup B)=P(A)+P(B)-P(A\cap B)`

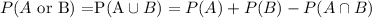
Since the total number od people in the table is equal to n=4089, we have that

`P(A)=(28+174+395)/(4089)=(597)/(4089)`

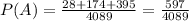
and

`P(B)=(174+194+71+179+173)/(4089)=\frac{791}{{4089}}`

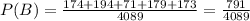
and

`P(A\cap B)=(174)/(4089)`

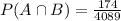
we have that

`P(A\text{ or B) =}(597)/(4089)+\frac{791}{{4089}}-(174)/(4089)`

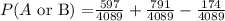
which gives

`P(A\text{ or B) =}(597+791-174)/(4089)=(1214)/(4089)=0.29689`

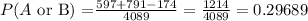
Therefore, the answer the searched probability is: 0.296