The volume of a Pyramid
Given a pyramid of base area A and height H, the volume is calculated as:
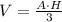
The base of this pyramid is a right triangle, with a hypotenuse of c=19.3 mm and one leg of a=16.8 mm. The other leg can be calculated by using the Pythagora's Theorem:

Solving for b:
![b^{}=\sqrt[]{c^2-a^2}=\sqrt[]{19.3^2-16.8^2}=9.5\operatorname{mm}]()
The area of the base is the semi-product of the legs:
![A=(16.8\cdot9.5)/(2)=79.8\operatorname{mm}^2]()
Now the volume of the pyramid:
![V=\frac{79.8\operatorname{mm}\cdot12\operatorname{mm}}{3}=319.2\operatorname{mm}^3]()
The volume of the figure is 319.2 cubic millimeters