Question

I am studying for the big test tomorrow and just need someone to go through this sheet I made with me.Sorry

Answer 1

Let us solve the simultaneous equation

`\begin{gathered} -2x-y=0 \\ x-y=3 \end{gathered}`

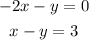
using elimination

To eliminate, we must decide which of the variables, x or y is easier to eliminate. The variable you must eliminate must be the same and have different sign. Looking above, it is easier to eliminate y because we have 1y above and 1y below. But to eliminate the y's, one must be +y and the other -y. So that +y -y becomes zero.

So to make the y's different, I will multiply the second equation by a -1. This becomes

`\begin{gathered} -2x-y=0 \\ (-1)x-y=3 \\ -2x-y=0 \\ -x+y=-3 \end{gathered}`

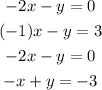
So, now we can eliminate y, doing this we have

`\begin{gathered} -2x-x=-3x \\ -y+y=0 \\ 0-3=-3 \\ \text{This becomes } \\ -3x=-3 \\ x=(-3)/(-3) \\ x=1 \end{gathered}`

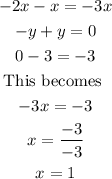
Now, to get y, we put x = 1 into any of the equations, Using equation 1, we have

`\begin{gathered} -2x-y=0 \\ -2(1)-y=0 \\ -2-y=0 \\ \text{moving -y to the other side } \\ y=-2 \end{gathered}`

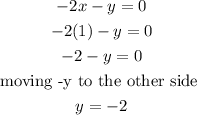
So, x = 1 and y = -2

Using substitution, we make y or x the subject in any of the equations. Looking at this, It is easier to do this using equation 2. From equation 2,

`\begin{gathered} x-y=3 \\ \text{making y the subject we have } \\ y=x-3 \end{gathered}`

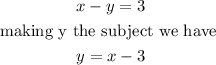
Now, we will put y = x - 3 into the other equation, which is equation 1, we have

`\begin{gathered} -2x-y=0 \\ -2x-(x-3)=0 \\ -2x-x+3=0 \\ -2x-1x+3=0 \\ -3x+3=0 \\ -3x=-3 \\ x=(-3)/(-3) \\ x=1 \end{gathered}`

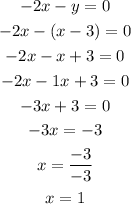
So, substituting x for 1 into equation 1, we have

`\begin{gathered} -2x-y=0 \\ -2(1)-y=0 \\ -2*1-y=0 \\ -2-y=0 \\ y=-2 \end{gathered}`

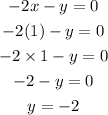
Substituting x for 1 into equation 2, we have

`\begin{gathered} x-y=3 \\ 1-y=3 \\ y=1-3 \\ y=-2 \end{gathered}`

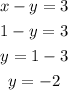
Now, for graphing,