Step 1
State the null and alternative hypothesis
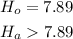
Step 2
State the p-value of the significance level.
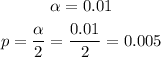
Step 3
Calculate the statistical test
![\begin{gathered} n=15 \\ \mu(\operatorname{mean})=11.09 \\ \sigma(s\tan dard\text{ deviation)=4.86} \end{gathered}]()
The t-test formula is given as
![t=\text{ }\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt[]{n}}}](https://img.qammunity.org/2023/formulas/mathematics/college/1uqnpt4jvs6e2x6w7bf6esq6c4ler4swm6.png)
Where
![\begin{gathered} \bar{x}=\operatorname{mean} \\ \mu=theoretical\text{ }value \\ \end{gathered}]()
![\begin{gathered} t=\frac{7.89-11.09}{\frac{4.86}{\sqrt[]{15}}} \\ t=(7.89-11.09)/(1.254846604) \\ t=(-3.2)/(1.254846604) \\ t=-2.550112492 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7ut8ia2jratkjdnd9327ki77ggj49klrqa.png)
Step 4
Find the p-value from the t-test.
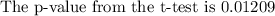
Step 5
Conclusion
The result is not significant at p<0.01. Therefore, the null hypothesis is rejected. It cannot be concluded that the mean in this area is higher than the national average because the p-value is greater than 0.01t