Question

A baseball is rolling along a tabletop with avelocity of 3.9 m/s to the right. The tabletopis 1.1 m above the ground. The ball rolls offthe edge of the table and falls to theground.A.) What is the ball's final vertical Velocity?B.) How long does the ball take to fall?C.) how far from the table does the ball land?

Answer 1

To answer this question we need to notice that once the ball starts falling we have a projectile motion; which means that horizontally we have a rectilinear motion and vertically we have an uniformly accelerated motion.

Then we can use the following equations for each direction:

`\begin{gathered} \text{ Horizontal motion:} \\ x=x_0+v_(0x)t \\ \text{ Vertical motion:} \\ a=(v_f-v_0)/(t) \\ y=y_0+v_0t+(1)/(2)at^2 \\ v_f^2-v_0^2=2a(y-y_0) \end{gathered}`

Since the ball is moving down in the vertical direction we will think that down is the positive direction vertically.

a)

We know that the ball is rolling to the right when it rolls off the edge of the table, this means that vertically the initial velocity is zero; we also know that the ball will fall for 1.1 m and that the acceleration is the gravitational acceleration. Then we can use the third vertical motion equation to find the final velocity, plugging the values we know we have that:

`\begin{gathered} v_f^2-0^2=2(9.8)(1.1) \\ v_f=√(2(9.8)(1.1)) \\ v_f=4.64 \end{gathered}`

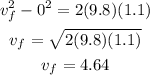
Therefore, the final vertical velocity is 4.64 m/s.

b)

To determine the time we can use the second vertical equation with the values we know:

`\begin{gathered} 1.1=0+0t+(1)/(2)(9.8)t^2 \\ 4.9t^2=1.1 \\ t^2=(1.1)/(4.9) \\ t=\sqrt{(1.1)/(4.9)} \\ t=0.474 \end{gathered}`

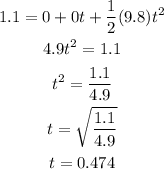
Therefore, it takes 0.474 s for the ball to fall.

c)

While the ball is falling it is also moving horizontally, in this direction we know the initial velocity is 3.9 m/s; using the horizontal equations we have:

`\begin{gathered} x=0+(3.9)(0.474) \\ x=1.85 \end{gathered}`

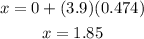
Therefore, the ball lads 1.85 m from the table.