Question

Factor out the greatest common factor. Simplify the factors, if possible.2(c + y)2 - 14(c+y)2 - 6(c+y)4Select the correct choice below and, if necessary, fill in the answer box to complete your choice.O A. 2(c+y) 3 – 14(c + y)2 - 6(c +y)4 =(Type your answer in factored form. Simplify your answer.)OB. There is no common factor other than 1.

Answer 1

The greatest common factor of a polynomial is the largest expression that divides all of the terms of the polynomial. In this case, we have:

`2(c+y)^3-14(c+y)^2-6(c+y)^4`

First, find the GCF of the coefficients of the terms. The coefficients are 2, 14 and 6, their GCF is 2.

On the other hand, notice that the factor (c+y) is a common factor for all three terms. Find the greatest power of (c+y) that divides all the terms. Since the lowest power of (c+y) in the expression is 2, then, the greatest power of (c+y) that divides all the terms is (c+y)^2.

The GCF of the expression is the product of the GCF of the coefficients and the GCF of the factors with variables.

Then, the GCF of the expression is:

`2(c+y)^2`

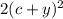
Factor out 2(c+y)^2 from the expression:

`2(c+y)^3-14(c+y)^2-6(c+y)^4=2(c+y)^2\lbrack(c+y)-7-3(c+y)^2\rbrack`

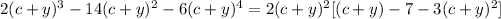
Therefore, the answer is option A and the expression inside the box should be:

`2(c+y)^2((c+y)-7-3(c+y)^2)`