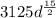Question

Hello, is it possible to show me the steps to simplify this problem? I don't understand the solution provided in my textbook.

Answer 1

Step-by-step explanation

We are asked to simplify the given question

`(\frac{75d^{(18)/(5)}}{3d^{(3)/(5)}})^{(5)/(2)}`

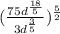
To simplify the terms, we will follow the steps below

Step 1: simplify the terms in the bracket using the exponential rule

Thus for the terms in the parentheses

`(\frac{75d^{(18)/(5)}}{3d^{(3)/(5)}})=(75)/(3)* d^{(18)/(5)-(3)/(5)}`

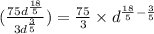
Hence

`25* d^{(18-3)/(5)}=25d^{(15)/(5)}=25d^3`

Simplifying further

`25d^3=25d^3`

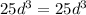
Step 2: substitute the value obtained above in step 1 into the parentheses, so that

`((75d^(18\/5))/(3d^(3\/5)))^{(5)/(2)}=(25d^3)^{(5)/(2)}`

Step 3: Simplify further, we will apply the rule

so that

`(25d^3)^{(5)/(2)}=25^{(5)/(2)}d^{3*(5)/(2)}`

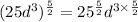
Simplifying further

`\begin{gathered} we\text{ will have} \\ √(25^5)* d^{(15)/(2)}=3125d^{(15)/(2)} \end{gathered}`

Hence, our final answer is

`3125d^{(15)/(2)}`