Question

In the triangle below, if B = 69°, A = 32°, c = 5.7, use the Law of Sines to find a. Round your answer to the nearest hundredth.

Answer 1

We know that the interior angles have to add to 180°, then we have that:

`\begin{gathered} C=180-69-32 \\ C=79 \end{gathered}`

Hence angle C=79°.

Now that we know the angle C we can use the law of sines to find a; the law of sines states that:

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

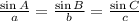
From this we have the equation:

`(\sin A)/(a)=(\sin C)/(c)`

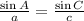
Plugging the values given and solving for a we have:

`\begin{gathered} (\sin32)/(a)=(\sin 79)/(5.7) \\ a=(5.7)(\sin 32)/(\sin 79) \\ a=3.08 \end{gathered}`

Therefore a=3.08