We know that the interior angles have to add to 180°, then we have that:
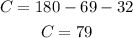
Hence angle C=79°.
Now that we know the angle C we can use the law of sines to find a; the law of sines states that:
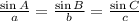
From this we have the equation:
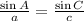
Plugging the values given and solving for a we have:
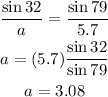
Therefore a=3.08