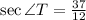Question

In ∆ STU, the measure of < U=90°, UT=12, SU=35, and TS=37. What ratio reprecents the secant of < T?

Answer 1

By definition, a Right triangle is a triangle that has an angle whose measure is 90 degrees (which is also called "Right angle").

You can identify that the triangle STU is a Right triangle, because:

`\angle U=90\degree`

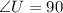
The following is one of the Trigonometric ratios. It's called "Secant":

`\sec \alpha=(hypotenuse)/(adjacent)`

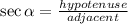
In this case you can identify that:

`\begin{gathered} \alpha=\angle T \\ hypotenuse=TS=37 \\ adjacent=UT=12 \end{gathered}`

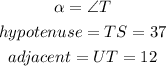
Then, substituting values, you get that the answer is:

`\sec \angle T=(37)/(12)`