Question

I need to know the initial size of the culture Find the doubling period Find the population after 65 min When will the population reach 10000

Answer 1

Given:

The population was 100 after 10 mins.

The population was 1500 after 30 mins.

To fill the blanks:

Step-by-step explanation:

According to the problem, we write,

`\begin{gathered} P=P_0e^(kt) \\ 100=P_0e^(10k).........(1) \\ 1500=P_0e^(30k)............(2) \end{gathered}`

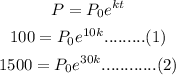
Dividing equation (2) by equation (1), we get

`\begin{gathered} (1500)/(100)=(P_0e^(30k))/(P_0e^(10k)) \\ 15=e^(20k) \\ ln15=20k \\ 2.708=20k \\ k=(2.708)/(20) \\ k=0.1354 \end{gathered}`

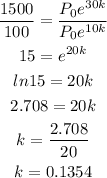
So, the equation becomes,

`P=P_0e^(0.1354t)....................(3)`

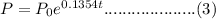
a) To find: The initial population

When P = 100 and t = 10, then the initial population would be,

`\begin{gathered} 100=P_0e^(0.1354(10)) \\ 100=P_0e^(1.354) \\ 100=P_0(3.873) \\ P_0=(100)/(3.873) \\ P_0\approx25.82 \end{gathered}`

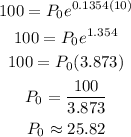
Therefore, the initial population is 25.82.

b) To find: The doubling time

Using the formula,

`\begin{gathered} t=(\ln2)/(k) \\ t=(\ln2)/(0.1354) \\ t=5.1192 \\ t\approx5.12mins \end{gathered}`

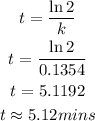
The doubling time is 5.12 mins.

c) To find: The population after 65 mins

Substituting t = 65 and the initial population is 25.82 in equation (3) we get,

`\begin{gathered} P=25.82e^(0.1354(65)) \\ P\approx171467.56 \end{gathered}`

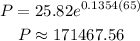
Therefore, the population after 65 mins is 171467.56.

d) To find: The time taken for the population to reach 10000

Substituting P = 10000 and the initial population is25.82 in equation (3) we get,

`\begin{gathered} 10000=25.82e^(0.1354t) \\ e^(0.1354t)=(10000)/(25.82) \\ e^(0.1354t)=387.297 \\ 0.1354t=\ln(387.297) \\ 0.1354t=5.959 \\ t=(5.959)/(0.1354) \\ t\approx44.01 \end{gathered}`

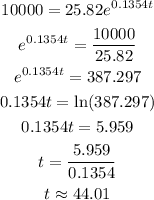
Therefore, the time taken for the population to reach 10000 is 44.01 mins.

Final answer:

• The initial population is 25.82.

,

• The doubling time is 5.12 mins.

,

• The population after 65 mins is 171467.56.

,

• The time taken for the population to reach 10000 is 44.01 mins.