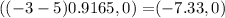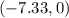Given:
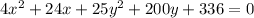
Aim:
We need to convert the given equation into the standard form of the ellipse equation.
Step-by-step explanation:
Consider the standard form of the ellipse equation.
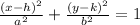
Consider the given equation.
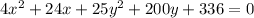
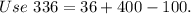
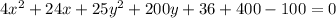
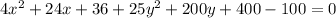
Take out the common terms.
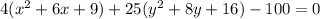
Add 100 on both sides of the equation.
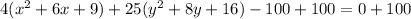
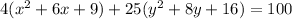
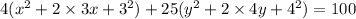
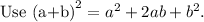
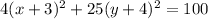
Divide both sides by 100.
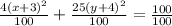
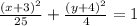
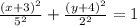
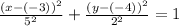
The standard form of the given equation is
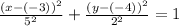
Compare with the general form of the ellipse equation.
We get h=-3, k=-4, a=5 and b=2.
The centre of the ellipse is h= -3 and k = -4.
The value of a is 5.
The value of b is 2.
We need to find the eccentricity of the ellipse.
![e=\sqrt[]{1-(b^2)/(a^2)}](https://img.qammunity.org/2023/formulas/mathematics/college/5roarepuhch1ugqdm9fv3j3zznhhopt20h.png)
Substitute b=2 and a =5 in the formula.
![e=\sqrt[]{1-(2^2)/(5^2)}=\sqrt[]{1-(4)/(25)}=\sqrt[]{(25-4)/(25)}=\sqrt[]{(21)/(25)}=0.9165](https://img.qammunity.org/2023/formulas/mathematics/college/7rk9mhhy37nem3tdp0eknqrndgfm0e7hcb.png)
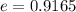
The foci of the ellipse are
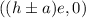
Substitute h =-3, a=5 and e =0.9165 in the formula.
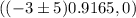
The foci with a positive x value are the point
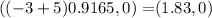
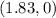
The foci with a negative x value are the point