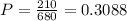Given 7 women and 10 men;
a) the top 3 are all men:
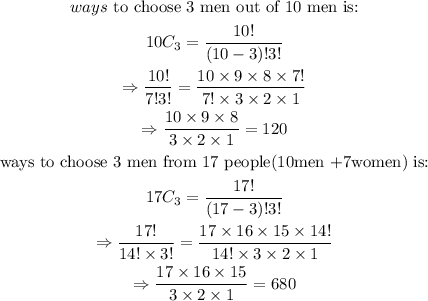
Therefore, the probability that the top 3 are all men is:
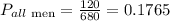
b) the top 3 are all women:
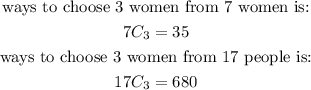
Therefore, the probability that the top 3 are all women is:
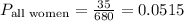
c) 2 men and 1 woman;
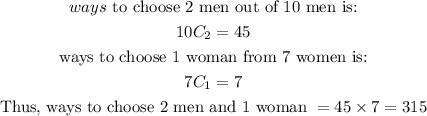
Therefore, the probability that the top 3 finishers are 2 men and 1 woman is:
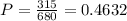
d) 1 man and 2 women;
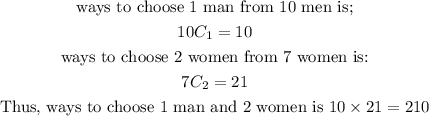
Therefore, the probability that the top 3 finishers are 1 man and 2 women is: