To find the area of the shaded region we need to calculate the area of the square and subtract to it the area of the circle.
The area of a square is calculated as follows:
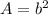
where b is the length of each side.
Substituting with b = 16 cm (given that the radius of the circle is 8 cm, then the length of the square's side is 2x8 = 16 cm):
![\begin{gathered} A_1=16^2 \\ A_1=256\operatorname{cm}^2 \end{gathered}]()
The area of a circle is calculated as follows:

where r is the radius of the circle.
Substituting with r = 8 cm, we get:
![\begin{gathered} A_2=\pi\cdot8^2 \\ A_2=\pi\cdot64 \\ A_2\approx201\operatorname{cm}^2 \end{gathered}]()
Finally, the area of the shaded region is:
![\begin{gathered} A_3=A_1-A_2 \\ A_3=256-201 \\ A_3=55\operatorname{cm}^2 \end{gathered}]()