Question

I believe the answer to be c but I'm not the best at word problems this is a practice study guide.

Answer 1

In order to find the interval of values where 95% of the shoe sizes lie, let's find the values of z-score that represents 2.5% to the left and 2.5% to the right of the standard distribution curve:

Looking at the z-table for the probabilities of 0.025 and 0.975, we have z1 = -1.96 and z2 = 1.96.

Now, we can calculate the values that define the interval using the formula below:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ -1.96=(x-8.1)/(1.47) \\ x-8.1=-2.88 \\ x=-2.88+8.1 \\ x=5.22 \\ \\ 1.96=(x-8.1)/(1.47) \\ x-8.1=2.88 \\ x=2.88+8.1 \\ x=10.98 \end{gathered}`

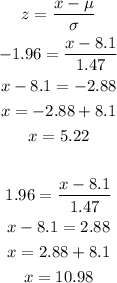
Therefore the correct option is the second one. (It's the only option with very close values to the ones calculated)