Question

stack of mail consists of 8 bills, 10 letters, and 6 advertisements. One piece of mail is drawn at random and put aside. Then a second piece of mail is drawn. Find P (both are letters)

Answer 1

INFORMATION:

We know that:

- stack of mail consists of 8 bills, 10 letters, and 6 advertisements.

- One piece of mail is drawn at random and put aside. Then a second piece of mail is drawn.

And we must find P (both are letters)

STEP BY STEP EXPLANATION:

To find the probability, we need to know that we have two events. First, when one piece of mail is drawn at random and put aside and, second, when a second piece of mail is drawn.

These two events are dependent. If A and B are dependent events, P(A and B) = P(A) • P(B after A) where P(B after A) is the probability that B occurs after A has occurred.

So, first

- Probability of A (the first piece is letter)

`P(A)=\frac{favorable\text{ }cases}{total\text{ cases}}=(10)/(24)`

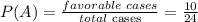
- Probability of B after A

Since A already occurred and one piece of the mail was drawn (a letter), now in total we would have 9 letter and 23 total pieces

`P(B\text{ after }A)=(9)/(23)`

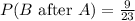
Finally, replacing in the initial formula

`P(A\text{ and }B)=(10)/(24)\cdot(9)/(23)=(90)/(552)=0.1630`

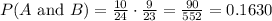
Finally, the probability would be 0.1630

ANSWER:

P (both are letters) = 0.1630