We can see here that the magnitude of the currents are:
 = 0.5263 A
= 0.5263 A
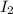 = 0.2632 A
= 0.2632 A
To calculate the currents,
 and
and
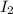 in the circuit, we can use Ohm's law (V = IR) and the rules of series and parallel circuits.
in the circuit, we can use Ohm's law (V = IR) and the rules of series and parallel circuits.
Where we have:
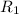 = 2.0 Ω
= 2.0 Ω
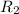 = 4.0 Ω
= 4.0 Ω
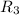 = 5.0 Ω
= 5.0 Ω
When resistors are connected in parallel, the reciprocal of the total resistance is the sum of the reciprocals of the individual resistances.
We have:
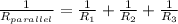
= 1/2 + 1/4 + 1/5
= 0.5 + 0.25 + 0.2 = 0.95
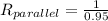 = 1.0526 Ω
= 1.0526 Ω
In a series circuit, the total current passing through the circuit is the same at any point.
Given that the ammeter reads 1.0 A, this represents the total current passing through the circuit.
Using Ohm's law (V = IR) and the total resistance calculated (1.0526 Ω) along with the total current (1.0 A), we can find the total voltage across the entire circuit.
Total voltage (V) = Total current (I) × Total resistance (R)
Total voltage (V) = 1.0 A × 1.0526 Ω ≈ 1.0526 V
As the resistors are in parallel, the voltage across each resistor is the same as the total voltage (1.0526 V), and we can use Ohm's law to find the currents,
 and
and
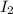 through
through
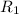 and
and
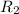 .
.
 = 1.0526 V/2.0 Ω = 0.5263 A
= 1.0526 V/2.0 Ω = 0.5263 A
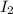 = 1.0526 V/4.0 Ω = 0.2632 A
= 1.0526 V/4.0 Ω = 0.2632 A