Question

What is the equation of the circle with endpoints (5,7) and (1,3)

Answer 1

`\text{Equation of circle: }(x-3)^2+(y-5)^2=\text{ 8}`

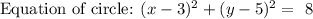
Step-by-step explanation:

endpoints (5,7) and (1,3)

The equation of circle formula:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ radius\text{ =r and (a, b) are the coordinates of the centre} \end{gathered}`

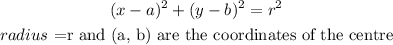
To find the centre(a, b), we need to find the midpoint of the two given points:

`\begin{gathered} \text{Midpoint = }(1)/(2)(x_1+x_2),\text{ }(1)/(2)(y_1+y_2) \\ \text{Midpoint = 1/2(5+1), 1/2(7+3)} \\ \text{Midpoint = 3, 5} \\ \text{centre = (a, b) =(3, 5)} \end{gathered}`

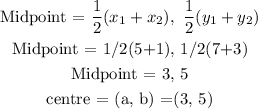
The radius is the distance between the centre of the circle and any of the two points.

We will apply the distance formula:

`\begin{gathered} dis\tan ce\text{ = }\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ (3,5)\text{ and (1, 3)} \\ \text{Distance =}\sqrt[]{(3-5)^2+(1-3)^2} \\ \text{Distance =}\sqrt[]{4+4} \\ \text{Distance =}\sqrt[]{8}\text{ = 2}\sqrt[]{2} \\ \text{radius = distance = 2}\sqrt[]{2} \end{gathered}`

Using the equation of circle:

`\begin{gathered} (x-3)^2+(y-5)^2=(2\sqrt[]{2)}^2 \\ (2\sqrt[]{2)}^2=\text{ }2\sqrt[]{2)}*2\sqrt[]{2)}\text{ = 4(}\sqrt[]{2})^2\text{ = 4(2) = 8} \\ (x-3)^2+(y-5)^2=\text{ 8} \end{gathered}`