Question

Which of the equation below could be the equation of this parabola

Answer 1

We have a parabola with the vertex at (0,0).

If we write the equation in vertex form, we have:

`\begin{gathered} \text{Vertex}\longrightarrow(h,k) \\ f(x)=a(x-h)^2+k \\ f(x)=a(x-0)^2+0=ax^2 \end{gathered}`

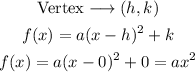
We have to find the value of the parameter a.

As the parabola is concave down, we already know that a<0.

As a<0 and y=a*x^2, the only option that satisfies this condition is y=-1/2*x^2.

Answer: y=-(1/2)*x^2 [Option C]