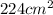Question

The ratio of the lengths of corresponding sides of two similar triangles is 5:8. The smaller triangle has an area of 87.5cm^2. What is the area of the larger triangle

Answer 1

Question:

Solution:

Remember the following theorem: the ratio of the areas of two

similar triangles is equal to the ratio of the squares of their corresponding sides. Then, here A1 and A2 are areas of two similar triangles, and S1 and S2 are their corresponding sides respectively :

S1 : S2 = 5 : 8

then

`(S1)/(S2)=(5)/(8)`

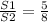
now, A1 = 87.5. Thus, according to the theorem, we get the following equation:

`((5)/(8))^2=(87.5)/(A2)`

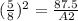
this is equivalent to:

`(25)/(64)=\text{ }(87.5)/(A2)`

by cross-multiplication, this is equivalent to:

`(A2)(25)\text{ = (64)(87.5)}`

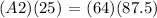
solving for A2, we get:

`A2\text{ =}((64)(87.5))/(25)=224`

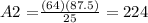
so that, we can conclude that the correct answer is:

The area of the larger triangle is

`224cm^2`