Question

The figure below is made up of a triangle and a circle. The ratio of the area of the triangle to the area of the circle is 5:6. If 1/5 of the area of the triangle is shaded, what is the ratio of the shaded area to the area of the figure?

Answer 1

`\begin{equation*} 1:10 \end{equation*}`

Step-by-step explanation

The ratio of the area of the triangle to the area of the circle is:

`5:6`

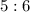
Let the area of the triangle be T.

1/5 of the area of the triangle is shaded i.e. 1/5 T

The total area of the figure is the sum of the area of the triangle that is not shaded and the area of the circle.

The area of the triangle that is not shaded is:

`\begin{gathered} T-(1)/(5)T \\ (4)/(5)T \end{gathered}`

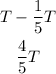
Let the area of the circle be C. The ratio of the area of the triangle to that of the circle is 5/6. This implies that:

`\begin{gathered} (T)/(C)=(5)/(6) \\ \Rightarrow C=(6T)/(5) \end{gathered}`

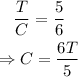
And so, the area of the figure is in terms of T is:

`\begin{gathered} (4)/(5)T+(6)/(5)T \\ 2T \end{gathered}`

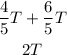
Therefore, the ratio of the shaded area to the area of the figure is:

`\begin{gathered} (1)/(5)T:2T \\ \Rightarrow(1)/(5):2 \\ \Rightarrow1:10 \end{gathered}`

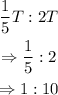
That is the answer.