Question

The average adult heart pumps about 84. mL/s of blood at 72 beats per minute. Suppose you need to calculate how long it would take the average heart tocirculate 6300. mL of blood.Set the math up. But don't do any of it. Just leave your answer as a math expressionAlso, be sure your answer includes all the correct unit symbols.

Answer 1

There are two ways to interpret the problem.

1) One is that a heart circulates 84ml of blood per second, although this makes the information of the beats per minute unnecessary.

In that case, an average heart would circulate 6300 ml of blood as shown in the next expression:

`\begin{gathered} 6300=84t \\ \Rightarrow t=(6300)/(84) \end{gathered}`

Where t is the time expressed in seconds

2) A second approach, and the one that makes better sense, is that each beat of the heart pumps 84ml per beat. Then, the expression that gives us the time needed to reach 6300ml of blood is:

`\begin{gathered} \frac{84ml}{\text{beat}},(72beats)/(\min ) \\ \Rightarrow84\cdot(72ml)/(\min)=(6048ml)/(\min ) \end{gathered}`

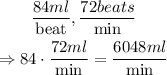
In that case, the equation that expresses the time needed by the heart to bump 6300ml of blood is:

`\begin{gathered} 6300=6048\cdot t \\ \Rightarrow t=(6300)/(6048) \end{gathered}`

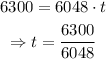
With t being the time given in minutes