SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given data
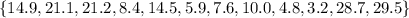
STEP 2: Find the mean ofthe data
![\begin{gathered} The\:arithemtic\:mean\:\left(average\right)\:is\:the\:sum\:of\:the\:values\:in\:the\:set\:divided\:by\:the\:number\:of\:elements\:in\:that\:set. \\ \mathrm{If\:our\:data\:set\:contains\:the\:values\:}a_1,\:\ldots \:,\:a_n\mathrm{\:\left(n\:elements\right)\:then\:the\:average}=(1)/(n)\sum _(i=1)^na_i\: \\ Sum=169.8 \\ n=12 \\ mean=(169.8)/(12) \\ mean=14.15 \end{gathered}]()
STEP 3: Find the median
![\begin{gathered} \mathrm{The\:median\:is\:the\:value\:separating\:the\:higher\:half\:of\:the\:data\:set,\:from\:the\:lower\:half.} \\ \:the\:number\:of\:terms\:is\:odd,\:then\:the\:median\:is\:the\:middle\:element\:of\:the\:sorted\:set \\ If\:the\:number\:of\:terms\:\:is\:even,\:then\:the\:median\:is\:the\:arithmetic\:mean\:of\:the\:two\:middle\:elements\:of\:the\:sorted\:set \\ \\ \mathrm{Arrange\:the\:terms\:in\:ascending\:order} \\ 3.2,\:4.8,\:5.9,\:7.6,\:8.4,\:10,\:14.5,\:14.9,\:21.1,\:21.2,\:28.7,\:29.5 \\ median=12.25 \end{gathered}]()
Hence, it can be seen here that the mean is larger than median.
STEP 4: Find the Interquartile range
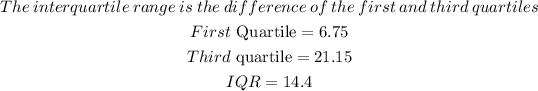
STEP 5: Find the standard deviation

Hence, it can be seen from above that the interquartile range is larger than the standard deviation.
STEP 6: Find the range
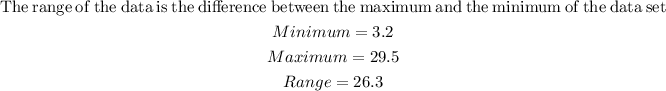
STEP 7: Fnd the variance
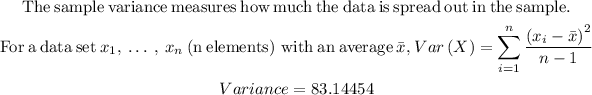
Hence, it can be seen that the range is not larger than the variance.
Therefore, the answer is I and II only.