Use the quadratic formula.
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where a = 3, b = -31, and c = -60.
![x=\frac{-(-31)\pm\sqrt[]{(-31)^2-4(3)(-60)}}{2(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/lm0ja7rwipw9rvczpavu4nxiyl26unh1j2.png)
Solve to find both solutions.
![x=\frac{31\pm\sqrt[]{961+720}}{6}=\frac{31\pm\sqrt[]{1681}}{6}=(31\pm41)/(6)](https://img.qammunity.org/2023/formulas/mathematics/college/rt9rnytlo2d1xjrtr8a59a58ppw2qxklpl.png)
Rewrite the expression as two.
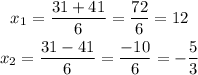
Once we have the solutions, we express them as factors. To do that, we have to move the constant to the right side of each equation.
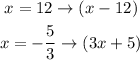
As can observe, the factor of the polynomial is (x-12).
Therefore, the answer is d.