First, let's calculate the number of different hands of 5 cards that can be made, using a combination of 52 choose 5:
(a standard deck card has 52 cards)
![C\left(52,5\right)=(52!)/(5!\left(52-5\right)!)=\frac{52\cdot51\operatorname{\cdot}50\operatorname{\cdot}49\operatorname{\cdot}48\operatorname{\cdot}47!}{5\operatorname{\cdot}4\operatorname{\cdot}3\operatorname{\cdot}2\operatorname{\cdot}47!}=\frac{52\cdot51\operatorname{\cdot}50\operatorname{\cdot}49\operatorname{\cdot}48}{120}=2,598,960]()
Now, let's calculate the number of hands that have 4 aces. Since the fifth card can be any of the remaining 48 cards after picking the 4 aces, there are 48 possible hands that have 4 aces.
Then, the probability of having a hand with 4 aces is given by the division of these 48 possible hands over the total number of possible hands of 5 cards:
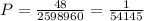
The probability is 1/54145.