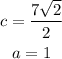Question

Special right trianglesFind the exact values of the side lengths c and a

Answer 1

Step-by-step explanation

First triangle

Since it is a right triangle, we can use the trigonometric ratio cos(θ) to find the length c.

`\cos(\theta)=\frac{\text{ Adjacent side}}{\text{ Hypotenuse}}`

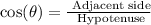
So, we have:

`\begin{gathered} \cos(\theta)=\frac{\text{ Adjacent side}}{\text{ Hypotenuse}} \\ \cos(45°)=(c)/(7) \\ \text{ Multiply by 7 from both sides} \\ \cos(45\degree)\cdot7=(c)/(7)\cdot7 \\ 7\cos(45\degree)=c \\ (7√(2))/(2)=c \end{gathered}`

Second triangle

Since it is a right triangle, we can use the trigonometric ratio cos(θ) to find the length a.

So, we have:

`\begin{gathered} \cos(\theta)=\frac{\text{ Adjacent side}}{\text{ Hypotenuse}} \\ \cos(60°)=(a)/(2) \\ \text{ Multiply by 2 from both sides} \\ \cos(60°)\cdot2=(a)/(2)\cdot2 \\ 2\cos(60\degree)=a \\ 2\cdot(1)/(2)=a \\ 1=a \end{gathered}`Answer
`\begin{gathered} c=(7√(2))/(2) \\ a=1 \end{gathered}`