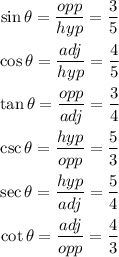The right angled triangle is given with reference angle theta.
The opposite side (facing the reference angle) is 3, while the hypotenuse (facing the right angle) is 5. The adjacent shall be calculated using the Pythagoras' theorem as follows;
![\begin{gathered} \text{Adj}^2+3^2=5^2 \\ \text{Adj}^2=5^2-3^2 \\ \text{Adj}^2=25-9 \\ \text{Adj}^2=16 \\ \text{Adj}=\sqrt[]{16} \\ \text{Adj}=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/55yg0irrorve79a2yohpulaqzrefmrkz6h.png)
Therefore, the trigonometric functions of angle theta are shown as follows;