We have the pH level as a random normal variable with mean 7.38 and standard deviation of 0.14.
A) We have to calculate the percentage of infants that are expected to have pH levels between 7.00 and 7.50.
We can approximate this as the probability of selecting a random infant and it has a pH level within this interval.
Then, to calculate the percentage we will use the z-scores for each boundary of the interval:
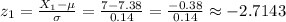
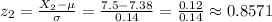
Then, we can use the standard normal distribution to look for the probabilities for each z-score and calculate the probability as:
![\begin{gathered} P(7.00Given that the probability is 0.80099, we can express the percentage as:[tex]P=0.80099\cdot100\%=80.01\%]()
B) We now have to calculate the percentage that is above 7.46.
We start by calculating the z-score as:

Then, we can calculate the probability as:

This correspond to a percentage of 28.39%.
Answer:
A) 80.01%
B) 28.39%