From the problem, two angles in a quadrilateral are 110 and 120 degrees.
Note that the sum of interior angles in a quadrilateral is 360 degrees.
Then the sum of the other two angles will be :
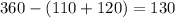
And the angles are in a ratio of 6 : 7.
Multiply the ratio by a common factor "x"
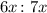
Then take the sum and equate it to 130 degrees.
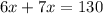
Solve for x :
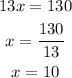
Now, substitute x = 10 to the ratio.
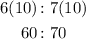
Therefore, the other two angles are 60 and 70 degrees.
ANSWER :
60 and 70 degrees