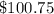Question

Jane has a pre-paid cell phone with NextFell. She can't remember the exact costs, but her plan has a monthly fee and a charge for each minute of calling time. In June she used 200 minutes and the cost was $75.00. In July she used 680 minutes and the cost was $195.00.

Answer 1

Explanation:

We will make use of algebra here.

First of all, we know that the monthly fee will be the same throughout all the months.
So, let's consider that cost to be the yet-to-find constant:
`a`.

A charge is accumulated for every minute on the call, so let's consider that minutely charge to be the constant:
`b`.

`x` is the number of minutes spent on the call.
So, the total charge after talking for
`x` minutes would be:

`b * x\\=bx`

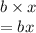
The monthly cost is the sum of the monthly fee and the total charge.

So, if this is represented mathematically, we get:

`C(x)= a+bx`

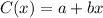
A piece of information that we have is that, after calling for 200 minutes (which means
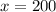`x=200`), the monthly cost (
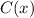`C(x)` ) would be $75.

Upon substituting these values in the equation we found above, we get:

`C(x)=a+bx\\\\75=a+200b`

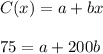
Similarly, we have another piece of information, which states that calling for 680 minutes (
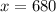`x=680`) produced a monthly cost of $195.

Upon substituting these values in the equation we found above, we get:

`C(x)=a+bx\\\\195=a+680b`

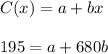
And, thus we have found a system of equations:

`a+200b=75\\a+680b=195`

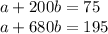
For the first equation, let's make
`a` the subject:

`a+200b=75\\\\a+200b-200b=75-200b\\\\a=75-200b`

Substitute this expression for
`a` into the second equation:

`a+680b=195\\\\75-200b+680b=195\\\\75+480b=195`

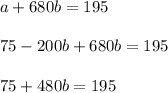
Find the value of
`b` using this equation:

`75+480b=195\\\\75+480b-75=195-75\\\\480b=120\\\\(480b)/(480)=(120)/(480)\\\\b=(1)/(4)`

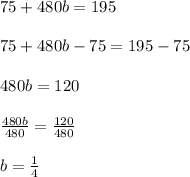
Insert the value for
`b` into the expression for
`a`:

`a=75-200b\\\\a=75-200((1)/(4))\\\\a=75-50\\\\a=25`

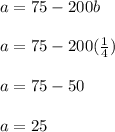
Since we have the values for the constants
`a` and
`b`, we can complete the function/equation
`C(x)`:

`C(x)=a+bx\\\\C(x)=25+(1)/(4)x`

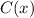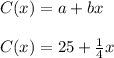
So, the answer for (A) is:

`C(x)=25+(1)/(4)x`

For (B), we have to find the monthly bill/cost (
`C(x)` ) when 323 minutes have been spent on calling.

So, we just have to substitute
`x` for 323, since
`x` represents the number of minutes spent on calling:

`C(x)=25+(1)/(4)x\\\\C(x)=25+(1)/(4)(323)\\\\C(x)=25+80.75\\\\C(x)=100.75`

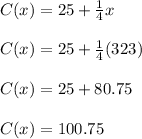
The answer for (B) is
`\$100.75`

Answer 2

We are given that Jane used 200 minutes and the cost was $75, and also she used 680 minutes and the cost was $195. To determine a function of the cost "C" as a function of the minutes "x" we will assume that the behavior of this function is that of a line. Therefore, the function must have the following form:

`C(x)=mx+b`

Where "m" is the slope and "b" the y-intercept. We will determine the slope using the following formula:

`m=(C_2-C_1)/(x_2-x_1)`

Where:

`(x_1,C_1),(x_2,C_2)`

Are points in the line. The given points are:

`\begin{gathered} (x_1_{},C_1)=(200,75) \\ (x_2,C_2)=(680,195) \end{gathered}`

Substituting in the formula for the slope we get:

`m=(195-75)/(680-200)`

Solving the operations we get:

`m=(120)/(480)=(1)/(4)`

Now we substitute in the formula for the line:

`C(x)=(1)/(4)x+b`

Now we determine the value if "b" by substituting the first point. This means that when C = 200, x = 75.

`200=(1)/(4)(75)+b`

Solving the product:

`200=18.75+b`

Now we subtract 18.75 from both sides:

`\begin{gathered} 200-18.75=b \\ 181.25=b \end{gathered}`

Therefore, the formula of the cost is:

`C(x)=(1)/(4)x+181.25`

Part B. We are asked to determine the cost is there is a consumption of 323 minutes. To do that we will substitute in the formula for "C" the value of x = 323.

`C(323)=(1)/(4)(323)+181.25`

Solving the operations we get:

`C(323)=262`

Therefore, the cost is $262.