Given:
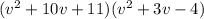
To find- the simplification.
Explanation-
We know that the distribution property of multiplication over addition says
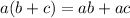
Use this property to simplify, and we get
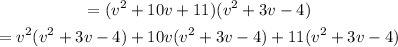
Multiply by opening the bracket, and we get
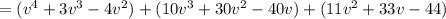
Now, open the bracket and combine the like terms.
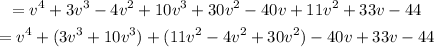
On further solving, we get
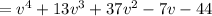
Thus, from the distributive property of multiplication over addition, we get v⁴+13v³+37v²-7v-44.
The answer is v⁴ + 13v³ + 37v² - 7v - 44.