Answer:
The correct answer is:
The ordered pair (2, 3) is not a solution to the system.
Step-by-step explanation:
The system given is:
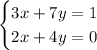
If (2, 3) is a solution of the system, then replacing x = 2 and y = 3 on both equations should give a correct result and the same on both equatiions.
In the first equation;
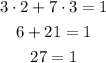
We can see that this result is not true, as 27 is not equal to 1.
In the second equation:
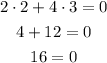
Once again, a false result.
To see in the system has equations, let's solve for x in the second equation:
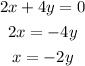
Now, we can use substitution in the first equation:
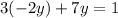
And solve for y:
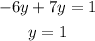
Now, we can find the value of x:
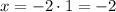
The solution to the system is (-2, 1)
Thus, the correct option is "The ordered pair (2, 3) is not a solution to the system"