SOLUTION
The following sequence is a geometric series and we have been provided with the formula
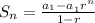
Here a1 is the first term = 40,
r is the common ratio = -0.4 (to get r, divide the second term by the first term)
n = number of terms = 9. Now let's solve
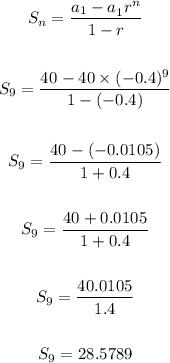
The sum to the nearest hundredth becomes = 28.58