Question

GRAPH each triangle and CLASSIFY the triangle according to its sides and angles.

Answer 1

`\Delta CAT\text{ is an ISOSCELES triangle}`

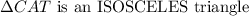
Step-by-step explanation:

To properly classify the traingle, we need to get the length of the sides

To get the length of the sides, we need to get the distance between each two points using the distance between two points formula

Mathematically,we have the formula as:

`D\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Where (x1,y1) refers to the coordiantes of the first point while (x2,y2) refers to the coordinates of the second point

let us get the coordinates of the individual points as seen from the plot shown

C (1,8)

A (5,10)

T (7,6)

So, let us find the distance between each two points

For AC, we have:

`D\text{ = }\sqrt[]{(5-1)^2+(10-8)^2}\text{ = }\sqrt[]{20}`

For AT, we have:

`D=\sqrt[]{(7-5)^2+(6-10)^2\text{ }}\text{ = }\sqrt[]{20}`

Lastly, for CT, we have:

`D\text{ = }\sqrt[]{(7-1)^2+(6-8)^2\text{ }}\text{ = }\sqrt[]{40}`

From our calculations, we can see that AC = AT

If we have a triangle which has two of its sides equal in length (the angle facing these sides would be same too), we call this an isosceles triangle

So, the class of triangle CAT is isosceles triangle