Answer:
Step-by-step explanation:
Given:
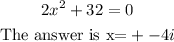
To fully understand how we get the given answer, we simplify the equation first:
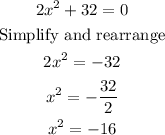
Next, we apply the rule:
![\begin{gathered} \text{For x}^2=f(a),\text{ the solutions are } \\ x=\sqrt[]{f(a)} \\ x=-\sqrt[]{f(a)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8gz7ppeg6m5m5cpnk5z9vyh3560mzoagaa.png)
So,
![\begin{gathered} x^2=-16 \\ x=\sqrt[]{-16},x=-\sqrt[]{-16} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fb81edz0um8wr53v0el2nlcyr5wz3erftn.png)
Then, we also apply the radical rule:
![\begin{gathered} \sqrt[]{-a}=\sqrt[]{-1}\sqrt[]{a} \\ So, \\ x=\sqrt[]{-16} \\ =\sqrt[]{-1}\sqrt[]{16} \\ \text{Then, apply the imaginary number rule:} \\ \sqrt[]{-1}=i \\ \text{Hence,} \\ x=4i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2j9i3cqjy4grk6jws5cmhpyq2n8r8ss3gq.png)
For
![\begin{gathered} x=-\sqrt[]{-16} \\ Use\text{ the same steps} \\ x=-4i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zwfaqbt8bj1mbkcat1mba59d57ad6tlunr.png)
Therefore the x-values are: x=4i, x=-4i. The i on the answer means imaginary number. It is a number that, when squared, has a negative result.