Question

While solving an equation 2x^2+32=0 the answer calculated is x=+-4i I understand the +- means the answer can be positive or negative but what does the i mean

Answer 1

Step-by-step explanation:

Given:

`\begin{gathered} 2x^2+32=0 \\ \text{The answer is x=}+-4i \end{gathered}`

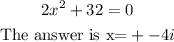
To fully understand how we get the given answer, we simplify the equation first:

`\begin{gathered} 2x^2+32=0 \\ \text{Simplify and rearrange} \\ 2x^2=-32 \\ x^2=-(32)/(2) \\ x^2=-16 \\ \end{gathered}`

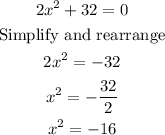
Next, we apply the rule:

`\begin{gathered} \text{For x}^2=f(a),\text{ the solutions are } \\ x=\sqrt[]{f(a)} \\ x=-\sqrt[]{f(a)} \end{gathered}`

So,

`\begin{gathered} x^2=-16 \\ x=\sqrt[]{-16},x=-\sqrt[]{-16} \end{gathered}`

Then, we also apply the radical rule:

`\begin{gathered} \sqrt[]{-a}=\sqrt[]{-1}\sqrt[]{a} \\ So, \\ x=\sqrt[]{-16} \\ =\sqrt[]{-1}\sqrt[]{16} \\ \text{Then, apply the imaginary number rule:} \\ \sqrt[]{-1}=i \\ \text{Hence,} \\ x=4i \end{gathered}`

For

`\begin{gathered} x=-\sqrt[]{-16} \\ Use\text{ the same steps} \\ x=-4i \end{gathered}`

Therefore the x-values are: x=4i, x=-4i. The i on the answer means imaginary number. It is a number that, when squared, has a negative result.