Given that

Step-by-step explanation
From the above, it is easy to see that the arrangement of the layers follows a geometric sequence where
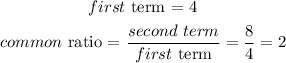
Since r>1, therefore the sum of 10 terms, which implies would give the total number of plates that are in the stack can be seen below.
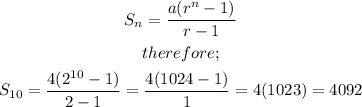
Answer: 4092