Question

There is a stack of plates in the backyard. There are 4 plates in the 1st layer, 8 in the second, 16 in the third, 32 in the fourth, and so on. There are total 10 rows/layers. How many total plates are in the stack?

Answer 1

Given that

`\begin{gathered} layer1=4plates \\ layer2=8plates \\ layer3=16plates \\ layer4=32plates \end{gathered}`

Step-by-step explanation

From the above, it is easy to see that the arrangement of the layers follows a geometric sequence where

`\begin{gathered} first\text{ term = 4} \\ common\text{ ratio = }\frac{second\text{ }term}{first\text{ term}}=(8)/(4)=2 \end{gathered}`

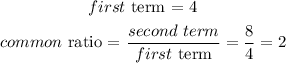
Since r>1, therefore the sum of 10 terms, which implies would give the total number of plates that are in the stack can be seen below.

`\begin{gathered} S_n=(a(r^n-1))/(r-1) \\ therefore; \\ S_(10)=(4(2^(10)-1))/(2-1)=(4(1024-1))/(1)=4(1023)=4092 \end{gathered}`

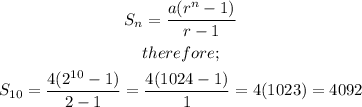
Answer: 4092