Question

Three vectors are shown in this figure. Their respective moduli are A = 4.00m.B = 3, 20m and C = 2.70mCalculate 2.00 A - B + 1.30 CExpress your answer according toa) Unit vectorsb) The modulus and orientation with respect to the positive part of the x-axis

Answer 1

Given that,

Modulus of vector A=4.00

The angle made by the vector A with the y axis, θ₁=33.0°

The modulus of vector B=3.20 m

The angle made by the vector B with the x-axis is θ₂=40.0+90.0=130°

The modulus of the vector C=2.70 m

The angle made by the vector C with x-axis θ₃=-90°

The x and y components of the vector can be written as

`\begin{gathered} x=r\cos \theta \\ y=r\sin \theta \end{gathered}`

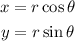
Where r is the magnitude (or modulus) of the vector and θ is the angle made by the vector.

Or a vector, in cartesian coordinates, can be written as,

`R=r\cos \theta\hat{\text{i}}+r\sin \theta\hat{j}`

Therefore, vector A is cartesian coordinates is

`\begin{gathered} \vec{A}=4.00\cos 33^(\circ)\hat{i}+4.00\sin 33.0^(\circ)\hat{j} \\ =3.35\hat{i}+2.18\hat{j} \end{gathered}`

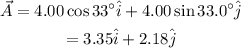
And the vector B is

`\begin{gathered} \vec{B}=3.20\cos (130^(\circ))\hat{i}+3.20\sin (130^(\circ))\hat{j} \\ =-2.06\hat{i}+2.45\hat{j} \end{gathered}`

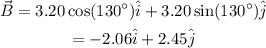
And vector C is given by,

`\begin{gathered} \vec{C}=2.70\cos (-90^(\circ))\hat{i}+2.70\sin (-90^(\circ))\hat{j} \\ =-2.7\hat{j} \end{gathered}`

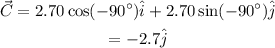
The given equation is

`2.00\vec{A}-\vec{B}+1.30\vec{C}`

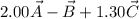
Let this represents a vector V

On substituting the known values,

`\begin{gathered} \vec{V}=2.00\vec{A}-\vec{B}+1.30\vec{C} \\ =2.00*(3.35\hat{i}+2.18\hat{j})-(-2.06\hat{i}+2.45\hat{j)}+1.30(-2.7\hat{j}) \\ =8.76\hat{i}-1.6\hat{j} \end{gathered}`

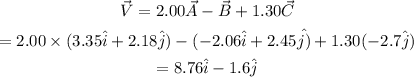
(a) This is the representation with the unit vectors, where i and j are the unit vectors along the x-axis and y-axis respectively.

`\vec{V}=8.76\hat{i}-1.6\hat{j}`

b) The modulus of any vector is the square root of the sum of the squares of its components.

That is, the magnitude of the vector V is

`\begin{gathered} V=\sqrt[]{8.76^2+(-1.6)^2} \\ =8.90\text{ m} \end{gathered}`

The angle of this vector with the x-axis is given by

`\begin{gathered} \phi=\tan ^(-1)((-1.6)/(8.75)) \\ =-10.36^(\circ)^{} \end{gathered}`

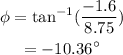
The negative sign indicates that the vector is below the positive x-axis

Therefore the modulus of the resultant of the above equation is 8.90 m and its angle with the positive x-axis is -10.36°