We can have more arguments to prove that PQRS is a rhombus, but, the argument that we will use here is:
Let's look at the first statement, we have

That's not correct, it would just prove that QR/2 > PS/2,
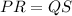
This statement implies
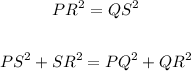
We cannot conclude that

The next statement is
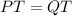
A rhombus can have different diagonals, and in fact they have. Then let's go to the next one

That also not exactly says it's a rhombus, it's a pallelogram property.

By doing that we have that the diagonal bissects the angle
That implies that the angle b is also bissect.
The last statment is
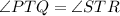
That's literally the vertex angle, it's true always, not only in that case, therefore the only possible answer is

Pro