Question

Jason enjoys watching the squirrels in his neighborhood park. They eat the red oak acorns. After the city removed 4 diseased red oak trees, the population of squirrels decreased from 105 to 98 in one year. If the population continues to decline at the same rate, how many squirrels will live in the park in 15 years? First, calculate the rate of decay by subtracting the two populations and dividing the difference by the initial population. Then, use the formula A=a0e^kt

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given parameters

`\begin{gathered} Initial\text{ squirrels}=105 \\ Num\text{ber of squirrels after one year}=98 \\ change\text{ in number of squirrels in a year}=105-98=7 \\ chan\text{ge in diseased oak trees}=y-4 \end{gathered}`

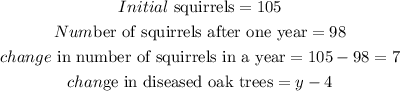
STEP 2: Calculate the rate of decay (k)

`\begin{gathered} rate\text{ of decay\lparen k\rparen}=\frac{Final\text{ population-Initial population}}{initial\text{ population}} \\ \text{By substitution,} \\ k=(98-105)/(105)=(-7)/(105)=-0.06666666\approx-0.0667 \end{gathered}`

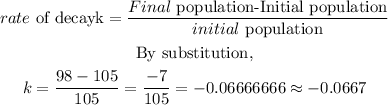
STEP 3: Calculate the number of squirrels after 15 years

`\begin{gathered} A=a_0e^(kt) \\ a_0=105 \\ k=-0.0667 \\ t=15 \end{gathered}`

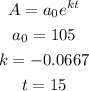
By substitution,

`A=105\cdot e^(-0.0667*15)`

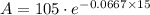
By simplification,

`\begin{gathered} \mathrm{Apply\:exponent\:rule}:\quad \:a^(-b)=(1)/(a^b) \\ =105* (1)/(e^(15* \:0.0667)) \\ \mathrm{Multiply\:fractions}:\quad \:a* (b)/(c)=(a\:* \:b)/(c) \\ =(1* \:105)/(e^(1.0005)) \\ \mathrm{Multiply\:the\:numbers:}\:1* \:105=105 \\ =(105)/(e^(1.0005)) \\ e^(1.0005)=2.71964 \\ =(105)/(2.71964) \\ \mathrm{Divide\:the\:numbers:}\:(105)/(2.71964)=38.60803 \\ =38.60803 \end{gathered}`

By approximation, this leaves us with 34 squirrels