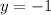1 Answer

Ask a Question

Cheriese · Answer 1 · 2023-07-18T20:02:03+0000

Step-by-step explanation:

We were given the function:

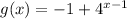
We are to determine its domain, range and horizontal asymptote. This is shown below:

Domain:

$\begin{gathered} g(x)=-1+4^(x-1) \\ 4^(x-1) \\ when:x=-10 \\ 4^(-10-1)=4^(-11) \\ when:x=1 \\ 4^^(1-1)=4^0=1 \\ when:x=20 \\ 4^(20-1)=4^(19) \\ \text{This shows us that the function is valid for every real number. This is written as:} \\ \left\x \end{gathered}$

Range:

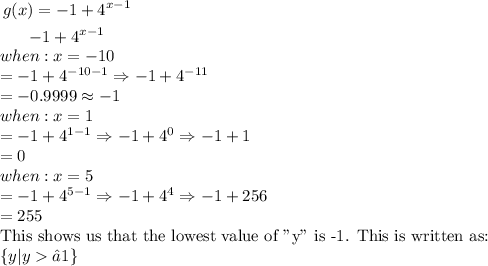
$\begin{gathered} g(x)=-1+4^(x-1) \\ \begin{equation*} -1+4^(x-1) \end{equation*} \\ when:x=-10 \\ =-1+4^(-10-1)\Rightarrow-1+4^(-11) \\ =-0.9999\approx-1 \\ when:x=1 \\ =-1+4^(1-1)\Rightarrow-1+4^0\Rightarrow-1+1 \\ =0 \\ when:x=5 \\ =-1+4^(5-1)\Rightarrow-1+4^4\Rightarrow-1+256 \\ =255 \\ \text{This shows us that the lowest value of ''y'' is -1. This is written as:} \\ \left\y>−1\right\ \end{gathered}$

Horizontal asmyptote:

For exponential functions, the equation of the horizontal asymptote is given as:

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions