Given: The line segment ST as shown in the image
To Determine: The bisector of ST and the value of ST
Solution
It can be observed from the first image, the bisector of ST is line MW
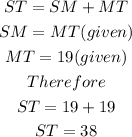
For the second image, the bisector of ST is line LM
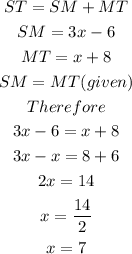
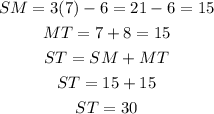
For first exercise, the bisector is MW, ST = 38
For the second exercise, the bisector is LM, ST = 30r