Question

A mass of 0.520 kilograms is attached to a spring and lowered into a resting position, causing the spring to stretch 18.7 centimeters. The mass is then lifted up and released. a. What is the spring constant of the spring? Include units in your answer.b. What is the frequency of its oscillation? Include units in your answer.Answer must be in 3 significant digits.

Answer 1

Given data

*The given mass is m = 0.520 kg

*The spring stretches at a distance is x = 18.7 cm = 0.187 m

*The value of the acceleration due to gravity is g = 9.8 m/s^2

(a)

The formula for the spring constant of the spring is given as

`\begin{gathered} F=kx \\ mg=kx \\ k=(mg)/(x) \end{gathered}`

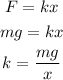
Substitute the known values in the above expression as

`\begin{gathered} k=((0.520)(9.8))/((0.187)) \\ =27.2\text{ N/m} \end{gathered}`

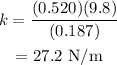
Hence, the spring constant of the spring is k = 27.2 N/m

(b)

The formula for the frequency of its